
 Share This Page
Share This Page| Home | | Science | |  |  |  Share This Page Share This Page |
Copyright © 2013, Paul Lutus — Message Page
Most recent revision: 03.02.2013
(double-click any word to see its definition)
At first glance, this article appears to be about a physics principle called the conservation of energy, i.e. "Energy is not created or destroyed, only changed in form". But the energy conservation principle only serves as an example, and this article has a higher purpose — it shows how shaping and testing theories creates scientific fields like physics.
Scientific fields don't spring into being because researchers perform experiments and publish papers — if that were true, astrologers could make astrology a science by simply hiring a lot of scientists. Instead, a scientific field is defined by its theories and established principles. A field's theories must be testable and potentially falsifiable in practical tests, and work in the field must address the field's defining theories.
This article will show how a description — "a perfectly insulated enclosure doesn't gain or lose heat energy" — can become a testable, general explanation, a scientific theory, by way of inductive generalization — "the total amount of energy in an isolated system remains constant over time." — and by that process can help define a scientific field.
Kinetic energy is the energy of motion — a thrown ball, a moving car, a spacecraft in orbit. The kinetic energy ek of a mass is equal to:
(1) $e_k = \frac{1}{2} m v^2$Where:
- ek = kinetic energy, joules
- m = mass, kilograms
- v = velocity, $\frac{meters}{second}$
Because this is about science, it would be nice if there were a convenient way to verify equation (1), using an everyday observation, especially the surprising fact that the energy of a moving mass is proportional to v2, the square of the velocity. Is it really true that an object has energy e at v, but has four times the energy (4 e) at 2 v?
Yes, it's true — concisely, double velocity, four times energy, and it's true about all moving masses. An example is a thrown baseball, which explains why the most skilled major-league pitchers rarely exceed 100 mph fastballs, and it's why a 100 mph fastball requires twice the throwing energy of a 71 mph ball.
Another example is wind velocity and wind energy. When we look at wind velocity charts, unless we know about the kinetic energy equation, we might think that a 100 mph wind is twice as powerful as a 50 mph wind. But in fact it's four times as powerful. This explains why automobile efficiency declines so quickly above 60 mph — the wind resistance begins to increase as the square of the car's velocity.
My favorite kinetic energy example is car stopping distances. Based on equation (1), it would seem that a car's kinetic energy should be proportional to the square of its speed. Is there any way to check this? Yes, as a matter of fact, there is — because of how car braking works, a skid mark's length is a linear measure of dissipated kinetic energy. This means each foot of a skid mark distance represents an equal amount of dissipated energy.
How does that relate to equation (1)? Well, it means that when you double a car's speed, its stopping distance becomes four times greater. Guess how many people know this about their cars.
Again, because this is about science, we should check this idea, compare it to real car stopping distances — see if it holds up. Let's start with the most basic experiment — let's pretend we know nothing about kinetic energy and want to rely on direct tests. So with that in mind I go to an empty parking lot and discover that my car requires 19 feet to stop from a speed of 20 mph (not including reaction time), and 76 feet at 40 mph. Based on my measurements, I can create a description of a stopping car, and I can use it to create a theory about car stopping distances.
With my field measurements and a little math, I create a predictive table of values for a range of car speeds (this table doesn't include driver reaction time):
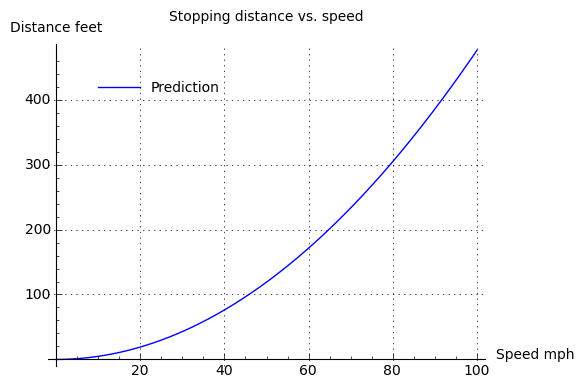
Speed mph Predicted stopping distance feet 10.00 4.76 15.00 10.71 20.00 19.05 25.00 29.76 30.00 42.86 35.00 58.33 40.00 76.19 45.00 96.43 50.00 119.05 55.00 144.05 60.00 171.43 65.00 201.19 70.00 233.33 75.00 267.86 80.00 304.76 85.00 344.05 90.00 385.71 Now that we have a table of predictions for speeds we haven't actually measured, we can consult an online source of data derived from field-measured stopping distances, and see how well our predictions hold up:
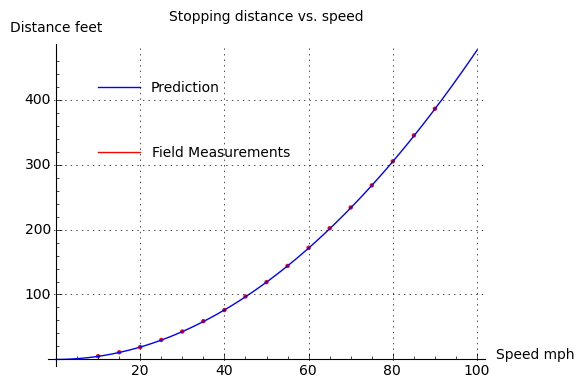
Speed mph Measured stopping distance feet 10 5 15 11 20 19 25 30 30 43 35 59 40 76 45 97 50 119 55 144 60 172 65 202 70 234 75 268 80 305 85 345 90 386 It appears we have confirmed our theory with field data. Now let's consider the sequence of events:
- A field measurement provides two data points that correlate vehicle speed and stopping distance.
- The experimental data are used to make a prediction about other speeds not actually measured.
- The prediction is successfully compared to field measurements for a range of speeds.
- The validation of the theory leads to its formal expression as the kinetic energy equation.
- Item (a) above is a simple field measurement — a description — that by itself cannot produce a theory about physics.
- Item (b) above makes an inductive, general explanation — a theory — based on a specific experiment.
- Item (c) above tests and confirms the theory using more field data.
- Item (d) above creates an equation that concisely expresses the theory we've tested.
All of the above steps are required for science, but only the last step can contribute to a field's corpus of tested theory, and to the definition of a scientific field.
Because we have moved from experiment to the level of theory, and because we have tested our theory, we have a reliable general statement about all masses in the universe — all of them follow the kinetic energy equation. This equation can make accurate statements about wind, water, planets and satellites, cars, and any other moving object.
The kinetic energy equation is just one in a group of central defining theories that define physics, and that make it a science.
My reason for explaining this in such detail is because there are fields that fancy themselves to be sciences, but that never get to steps (b) through (d) in the above list. Such fields never generalize observations, test the generalizations, or craft theories that would place their field on a solid scientific foundation. Such fields are sciences in name only.
Potential energy is the energy of position or state. Everyday examples include a charged battery or a book on a high shelf. The electrical charge of a fully charged Alkaline D-cell battery is about 74,970 Joules or 20.83 watt-hours (source).
If we pick up a book from the floor and put it on a high shelf, we have added some gravitational potential energy (hereafter GPE) to the book (or, more precisely, to the system consisting of the book and the Earth), based on this equation:
Note that GPE is negative — as two masses approach each other, their mutual GPE becomes more negative. This convention is essential to computing gravitational interactions, for these reasons:(2) $e_p = \frac{-G m_1 m_2}{r}$
Where:
- ep = GPE, joules
- G = gravitational constant, equal to $6.67384 \times 10^{-11} N \, m^2 kg^{-2}$
- m1 = mass 1, kilograms
- m2 = mass 2, kilograms
- r = radius between m1 and m2, meters.
- Because increasing the radius between two masses requires an expenditure of energy, the result should be a positive change in the system's potential energy, but
- Two masses separated by an infinite distance should have zero GPE, therefore
- GPE values are always ≤ 0.
We will revisit the issue of negative GPE and the reasoning behind it.
Suppose we pick up a book from the floor (on Earth) and place it on a two meter high shelf. Suppose also that the book weighs one kilogram. We proceed as follows:
(3) $e_p = \frac{-G m_1 m_2}{r} = \frac{-G m_e m_b}{r_e + y} - \frac{-G m_e m_b}{r_e} = \frac{G m_{b} m_{e} y}{r_{e}^{2} + r_{e} y}$ = 19.645 J
Where the new undefined terms are:
- me = mass of earth, $5.9736 \times 10^{24}$ kg
- mb = mass of book, 1 kg
- re = radius of earth, $6.371 \times 10^6$ meters
- y = changed height of book, 2 meters.
In the case of kinetic energy discussed earlier, the energy added to the system is represented by the velocity of the mass. But where is potential gravitational energy located? We lifted a book in a gravitational field, adding potential energy to the system, but where is the added energy located?
The answer is that potential energy is represented by mass — each increase in potential energy increases mass, according to the mass-energy equivalence equation with which most people will be familiar:
(4) $E = m c^2$
Where:
- E = energy
- m = mass
- c = speed of light, 299,792,458 m/s
Therefore, by lifting a book through 2 meters and giving it an increased energy of 19.645 J, we have given it an increased mass of:
(5) $E = m c^2 \therefore m = \frac{E}{c^2} \therefore \frac{19.645}{c^2} = 2.2 \times 10^{-16} kg$A very small mass indeed, about 1/3 that of a small bacterium.
At this point we've established the following principles:
- In a closed system, energy is constant over time.
- Kinetic energy is the energy of motion.
- Potential energy is the energy of position or state.
- GPE is present between masses, and as the masses approach, GPE decreases.
Planetary orbits are an excellent example of the principle of energy conservation, because over time, a mass in an elliptical orbit (most orbits are elliptical) converts energy from potential to kinetic and the reverse, while maintaining a constant total energy (the sum of potential and kinetic energy). Also, orbital observations — experimental confirmations — are relatively easy to carry out.
Here's a summary of the energy equations relevant to an orbit:
An orbiting body's kinetic energy is:
(6) $e_k = \frac{1}{2} m v^2$
Its GPE is:
(7) $e_p = \frac{G m_1 m_2}{r}$
According to the principle of energy conservation, for an orbit in a vacuum where we can assume no friction exists, the system's total energy et must be constant, and is the sum of kinetic and potential energy, or:
(8) $e_t = e_k + e_p = \frac{1}{2} m v^2 + \frac{G m_1 m_2}{r}$Notice about equation (8) that we're assuming only one of the two masses is in motion. This assumption is optional — the physics is consistent regardless of how the kinetic energy is pictured as distributed between the two masses, but making this assumption simplifies the calculation.
Aware that a picture is thought to be worth $1 \times 10^3$ words, I have written a numerical orbit simulator to show that energy is conserved. Click within the image below to see the result.
Click below to start or stop the animation.
Swept area: 0 Kinetic energy ek: 0 Potential energy ep: 0 Total energy et: 0 This orbital simulator is realistic enough to show that, as the orbit proceeds and as the orbiting body appraches and recedes from the parent body, the ever-changing relationship between kinetic and potential energy produces a constant sum ("Total energy" above), consistent with the principle of energy conservation.
One of the earliest insights into planetary orbits was made by Johannes Kepler, whose second law says, "A line joining a planet and the Sun sweeps out equal areas during equal intervals of time." This simulation shows agreement with this law (see the green ellipse segment and the "Swept area" value below the animation), apart from a small deviation that results only from limited numerical precision.
Indeed, it seems Kepler's second law contains within it the idea of energy conservation, although Kepler lived long before anyone formalized the idea of energy conservation. In this equivalence, the radius of the green ellipse segment represents potential energy, and its width (its subtended angle) represents kinetic energy. Put another way, the statement that orbital energy is conserved, and Kepler's second law, say the same thing.
Notes on the animation: The orbital simulator uses a relatively new Web (HTML5) feature called "canvas", a simple and efficient way to add animations to a Web page. Unfortunately, as is so often the case, Microsoft's browser doesn't support canvas and must be coerced into supporting it in a somewhat crippled way. If the simulation is slow and you're using Microsoft's browser, by all means install a different browser — any other browser. Browsers that run this simulation blazingly fast include Chrome and Firefox.
Apart from explaining the principle of conservation of energy, my purpose in this article is to show how scientific fields function — how they depend on the existence of testable principles and theories to unify research efforts within the field, as well as confer legitimate scientific status to the field.
Can a field be scientific without established, testable principles and theories? No, not really. Without theories, it's not obvious what the field would mean — what context would exist to guide research.
In a physics context, for example, a new idea that contradicted the principle of energy conservation would have to be accompanied by substantial evidence and an alternative explanation for the many observations that appear to support energy conservation.
Fields without central defining theories (i.e. psycholgy, sociology and others) don't have this problem — if a new idea comes along, it doesn't have to show how it works within, or contradicts, a pre-existing theoretical framework, for the simple reason that there's no such framework. This makes life very easy for psychologists, who, by wandering in a theoretical vacuum, can say or do practically anything.
This indifference to theoretical issues wouldn't be a problem for psychology any more than it is for philosophy, except for one thing — unlike philosophers, psychologists have clinics and pose as mental doctors to a gullible public.
But because of an absence of tested theories to define and discipline psychology, there is no mental medicine to stand alongside physical medicine, as a result of which, in spite of the existence of mental health clinics everywhere, there aren't actually any mental doctors to stand alongside physical doctors — the people who occupy mental health clinics are each more or less effective soley based on their personal skills, not because of their status as psychologists.
This article shows how physicists solve problems, how physics works, and why it is a science. Physics is a science only because of the existence of well-tested physical theories, as well as constant research to refine and sometimes falsify physical theories.
Physical theories have properties that legitimate scientific theories are expected to have — objectivity, meaning different observers will come to the same conclusion, falsifiability, meaning new persuasive evidence can overthrow existing theories, and consistency, meaning different physical theories must not contradict each other.
This article's orbital example shows how a planetary orbit requires three elements of physical theory to be both true and consistent:
- (9) Kinetic energy must be equal to: $e_k = \frac{1}{2} m v^2$
- (10) GPE must be equal to: $e_p = \frac{-G m_1 m_2}{r}$
- (11) Total orbital energy must be constant: $e_t = e_k + e_p = \frac{1}{2} m v^2 + \frac{-G m_1 m_2}{r}$
The three elements are defined by different underlying physical principles (kinetic energy, potential energy, and conservation of energy), and their ability to work together as well as model nature shows that physical theory is internally consistent as well as empirical. This is why physics is a science — not because of big research budgets, not because of impressive laboratories, not because of white lab coats, but because of theories that are consistent with each other and with nature, theories that define physics.
I regularly hear from psychologists who object to my frequent comparisons of psychology to real science, who try to say there are different kinds of science (and there are — there's science and pseudoscience), who ask why this is all so important. Isn't psychological science good enough?
In reply, I ask whether psychologists intend to pose as mental doctors, tell us what's wrong with us, estimate how many of us are "mentally ill" and how that number seems inevitably to increase as the years go by. If psychologists want to be thought of as doctors, then to avoid more disasters like Recovered Memory Therapy, psychologists must adopt scientific methods. And if they can't or won't do that, they need to stop pretending to be either scientists or doctors.
- Conservation of Energy — "Energy is not created or destroyed, only changed in form."
- Kinetic energy — the energy of motion.
- Potential energy — the energy of position or state.
- Inductive Generalization — a logical step whereby an experimental outcome is proposed as a general explanation.
- Wind Energy — the kinetic energy of wind.
- Vehicle Stopping Distance And Time — an online table of stopping distances derived from field measurements.
- Battery Data — shows the electrical energy stored in some commmon battery types.
- Gravitational potential energy — the energy associated with a gravitational field.
- Gravitational constant — an empirical physical constant used in gravitational work.
- Mass-energy equivalence — the statement that mass is a measure of energy, and vice versa.
- Speed of light — an important physical constant.
- Johannes Kepler — pioneering astronomer, from a time when it was dangerous to make claims the Church didn't like.
- Kepler's laws of planetary motion — an early effort to craft a theory of orbits.
- False memory syndrome — the outcome of Recovered Memory Therapy.
| Home | | Science | |  |  |  Share This Page Share This Page |