
 Share This Page
Share This Page| Home | | Science | |  |  |  Share This Page Share This Page |
This article's goal is to give nonspecialist readers an intuitive grasp of some easily understood aspects of relativity theory, in particular the relationship between space and time. No specialized knowledge is assumed apart from some high-school mathematics.
To help convey relativity's key ideas, to the extent possible the theory's ideas are modeled with graphics and animations. It's my hope that, rather than replacing mathematical ideas, the visual aids will make the mathematics easier to understand.
It is often said that, when writing for a popular audience, each included equation cuts one's readership in half. It's my hope that the promise of some insight into relativity theory will suspend this rule.
Let's start with a bit of history. In 1905 Albert Einstein published his first relativity paper (On the electrodynamics of moving bodies, A. Einstein, 1905), in which he described a theory later known as Special Relativity. In Part I of his paper Einstein included a number of equations meant to quantify the relationship between space and time "velocities" and dimensions. Here's a key equation from Einstein's paper:
(1) $ \beta = \frac{1}{\sqrt{1-v^2/c^2}}$
Where:
- v = space velocity
- c = speed of light
- β = a dimensionless term that quantifies changes in space and time at velocity v
At the time Einstein published his paper, he was able to use such equations to predict changes in time "velocity" and spatial dimensions that would result from provided space velocities. But when Einstein's math teacher Hermann Minkowski read his former student's paper, he noticed something Einstein did not — Minkowski realized the equations united space and time in a four-dimensional entity Minkowski called spacetime. About this realization, Minkowski later said, "Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality."
To see what Minkowski saw, let's write a simpler version of equation (1) that includes terms for space (v) and time (t) velocities:
(2) $c^2 = t^2 + v^2$
Where:
- c = speed of light
- t = time "velocity"
- v = space velocity
Those familiar with geometry will recognize that equation (2) can be used to describe the relationship between a right triangle's hypotenuse (c) and its other two sides (t and v), based on the Pythagorean Theorem. Using this equation, the relationship between space (v) and time (t) velocities is easily derived:
Figure 1: Interactive spacetime diagram(3) $v^2 = c^2 - t^2$
(4) $t^2 = c^2 - v^2$
Based on equations (3) and (4), if c is held constant, we see that any increase in v must cause a decrease in t — they're bound together in such a way that their combined values must produce this constant result:
(5) $c = \sqrt{t^2 + v^2}$Examine Figure 1 and notice about variables v (space) and t (time) that they're at right angles to each other — they lie in different dimensions.
If your browser supports the "canvas" feature, you may drag your mouse cursor horizontally across Figure 1 and notice that:
- The c value, the speed of light (and the hypotenuse length), remains constant (a requirement of relativity theory).
- When space velocity v increases, time velocity t decreases.
Figure 1 shows the relationship between space and time velocities in special relativity — when v equals 0, when there is no space velocity, the "velocity" of time equals c, the speed of light. Conversely, when space velocity equals c, there is no time velocity — time has stopped. This leads to these points:
- The special relativity equations imply that space and time represent related dimensions in spacetime (three dimensions for space, one for time).
- In relativity theory, the speed of light defines the relationship between the space and time dimensions.
- Relativity theory requires that c (the speed of light) remain constant in all frames of reference, therefore (as shown in Figure 1) any increase in space velocity must produce a decrease in time velocity.
- Figure 1 shows that, when space velocity equals zero, time's "velocity" is the speed of light.
- At all nonzero space velocities, time's velocity declines proportionally.
- If we somehow could move at the speed of light, time would stop.
- For reasons provided in the next section, objects with mass can't approach the speed of light.
- Photons, the carrier particles of the electromagnetic field, have no mass and do travel at the speed of light, as a result of which they don't experience time.
Let's look at some consequences of the space and time changes described above.
Time changes
Imagine that astronauts on board a spacecraft (call it spacecraft b) are traveling at a speed of $\frac{1}{2} c$. According to the equations above, the rate at which time passes should be:
(6) $t' = t \sqrt{1 - v^2/c^2} = \sqrt{1 - (1/2)^2} = 0.866 t$
Where:
- t = time rate at velocity 0
- t' = time rate at velocity v
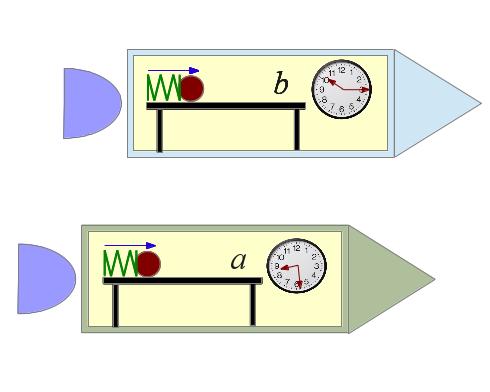 Figure 2: Spacecraft in relative motion
Figure 2: Spacecraft in relative motionEquation (6) means that, for astronauts traveling at $\frac{1}{2} c$, because of relativistic time dilation the passage of an hour should require 69 minutes and 17 seconds. Can the astronauts in spacecraft b detect this time change? Well, no, they can't — their clocks will slow down, their heartbeats will slow down, even supremely accurate atomic clocks will slow down, all in step. This means any tests the astronauts conduct within spacecraft b will show perfect agreement between various sources of information about the passage of time.
However, if astronauts on a relatively stationary spacecraft (call it spacecraft a) were to observe the clocks on board spacecraft b, by comparing their own clocks with those on board the moving spacecraft, they would notice spacecraft b's time dilation — indeed, they could use the time difference to determine spacecraft b's velocity relative to their own.
Mass changes
The above equations rule out travel at the speed of light, using this reasoning:
- In space, in the absence of gravity, an object's mass is measured by its resistance to changes in speed (acceleration) — more massive objects require more force (or more time) to change their speed.
- Imagine an experiment aboard spacecraft b that pushes a mass with a spring that exerts a known force, as in Figure 2. The experiment should be able to measure the object's mass, based on this expression of Newton's second law of motion:
(7) $m = \frac{f}{a}$
Where:
- m = mass, kilograms
- f = force, Newtons
- a = acceleration, meters per second
According to equation (7), if a mass is pushed by a one-Newton force for one second, and accelerates to a speed of one meter per second, the object has a mass of one kilogram.
- Let's say the astronauts aboard spacecraft b conduct this experiment and determine that an object has a mass of one kilogram.
- Let's also say the astronauts aboard spacecraft a observe the experiment aboard spacecraft b, but a's crew comes to a different conclusion. In the frame of reference of spacecraft a and because of spacecraft b's time dilation, the mass aboard spacecraft b only acquired a speed of 0.866 meters per second, therefore it weighs:
This result means that, at a velocity of $\frac{1}{2}c$, masses on board spacecraft b weigh 15% more.(8) $m' = \frac{m}{\sqrt{1 - v^2/c^2}} = \frac{m}{\sqrt{1 - (1/2)^2}} = 1.154 m$
Where:
- m = mass at velocity 0
- m' mass at velocity v
- Does this relativistic mass increase have any practical consequences? Yes, it does — the experimental mass weighs more, but so does the entire spacecraft. In order to get to its destination, the spacecraft's engines have to deliver more power to accelerate the heavier spacecraft.
- Let's imagine a more extreme example. Let's say we want to move at 99% of the speed of light. The time dilation for this speed is:
(9) $t' = t \sqrt{1 - v^2/c^2} = \sqrt{1 - 0.99^2} = 0.141 t$
This means an hour aboard spacecraft b requires seven hours and five minutes aboard spacecraft a (but the astronauts on board spacecraft b subjectively experience one hour of time).
- At 0.99c, the mass change is:
(10) $m' = \frac{m}{\sqrt{1 - v^2/c^2}} = \frac{m}{\sqrt{1 - 0.99^2}} = 7.08 m$
This means, for a given acceleration, the spacecraft's engines must deliver seven times more power. And as the spacecraft moves closer to the speed of light, its mass increases without bound and the power required to increase speed also increases without bound.
- At the speed of light, the above equations break down — they indicate a time rate of zero and an infinite mass.
- This is why massive objects cannot travel at the speed of light.
Readers may wonder whether the mass increase is real — isn't it a coincidental side effect of time dilation, with no independent reality? The answer is that both the time and mass effects are real and interchangeable — one can derive time dilation from mass increase or vice versa. Both interpretations are equally valid.
Spacetime interval
Hermann Minkowski's contribution to relativity theory — his spacetime interpretation — changed how we picture the relationship between causes and effects. We now know there is a clear demarcation between effects and their possible causes, and the speed of light is the gatekeeper. Expressed simply, if a cause at spacetime location a can propagate to spacetime location b at less than or equal to c (the speed of light), then cause a may produce effect b, otherwise not. To understand this, we need to introduce the idea of a spacetime interval:
(11) $s^2 = \Delta r^2 - c^2 \Delta t^2$
(12) $\Delta r = r_a - r_b$ (space difference)
(13) $\Delta t = t_a - t_b$ (time difference)
Where:
- s = four-dimensional spacetime interval
- c = speed of light
- $r_a$ = spatial location of event a
- $r_b$ = spatial location of event b
- $t_a$ = temporal location of event a
- $t_b$ = temporal location of event b
Because a spacetime interval takes both space and time dimensions into account and with respect to causes and effects, its meaning is unambiguous:
Value of s2 Basis Comment $s^2 \lt 0$ $\Delta r^2 \lt c^2 \Delta t^2$ Time-like interval: Cause a can produce effect b $s^2 = 0$ $\Delta r^2 = c^2 \Delta t^2$ Light-like interval: Cause a can produce effect b $s^2 \gt 0$ $\Delta r^2 \gt c^2 \Delta t^2$ Space-like interval: Cause a cannot produce effect b Light cone diagram
Because visualizing four-dimensional spacetime intervals may be difficult at first, readers may want to play with Figure 3, an interactive light cone diagram — change the viewing angle and size with your mouse:
Anaglyphic () mode: Inverted (black background):
Figure 3: Interactive light cone diagramSome notes on Figure 3:
- This resource is much better viewed in 3D, using anaglyphic
glasses.
- The green plane at the center represents the space dimensions and the present time.
- The axis perpendicular to the green plane represents the time dimension.
- The central point o, where the cones intersect, is the "origin", the present location and time — the x,y,z (space dimensions) and t (time dimension) all equal zero.
- It's helpful to picture the past and future cones as expanding into the space dimensions at the speed of light as they extend through time:
- Spacetime coordinate points a - e in Figure 3 are located at the same space position, but different time positions.
- Spacetime coordinate c is located in the present (it's on the surface of the green plane), but is separated from the origin o by a spatial distance, therefore it cannot influence events at the origin o.
- Coordinate b has the same space position as c, but a different time position. Because coordinate b is outside the past light cone, like coordinate c it cannot influence events in the present.
- Coordinate a has the same space position as c, but it's located farther in the past than b. Because coordinate a is inside the past light cone, it can influence events in the present.
- The same relationship applies to coordinates d and e — coordinate d, located outside the future light cone, cannot be influenced by events in the present, but coordinate e can.
Causality
Causality, the relationship between causes and effects, is a central issue in physics, and the plausibility of a new theory can be measured in part by whether it allows effects to precede their causes. For example, some readings of General Relativity allow violations of causality, and those issues are a matter of much debate. There is no experimental confirmation of these effects, and such confirmation is unlikely.
There are quantum effects such as entanglement that, at first glance, allow for instantaneous communication at superluminal speeds, but as it turns out, this isn't so — entanglement really does cause two particles to interact at any distance, but this fact cannot be used to circumvent limitations posed by the speed of light.
Special vs. general relativity
Special relativity deals with a subset of physical effects — those that don't involve accelerations. General relativity is a much broader theory, and because of its scope and experimental confirmations, it is regarded by some as the crowning achievement of twentieth century physics.
In order for special relativity to explain effects that prior theories could not, it had to contradict certain assumptions about everyday reality like the idea that time is the same for everyone. General relativity follows this pattern, but because it explains more, it contradicts more common-sense assumptions.
In the prior special relativity section we saw that quantities like velocity, time and mass depend on one's reference frame, but in the midst of these perceptions, space retained its overall shape. In general relativity, the shape of space itself is a term in the equations and depends on one's frame of reference. One might say that in general relativity, there's more relativity.
In special relativity, a force called gravity pulls the moon in a curved orbit around the earth. In general relativity, gravity isn't a force, and the moon moves in a straight line through curved spacetime.
Figure 4: Gravitational starlight deflectionIn special relativity, only objects possessing mass feel the force of gravity, and massless particles like photons travel in straight lines through a space that has no role in gravitation. In general relativity, as physicist John Wheeler famously said, "Matter tells space how to curve. Space tells matter how to move."
Spacetime curvature: starlight deflection
When Einstein published general relativity in 1916, because it had no experimental confirmation it was met with healthy skepticism. In an effort to make his theory less theoretical and more empirical, Einstein suggested that a field of stars be photographed during a solar eclipse and compared to the same field without the effect of the sun. The idea is that spacetime curvature near the massive sun should change the apparent positions of those stars nearest the sun (Figure 4).
Figure 5: Optical lens geometryAfter a number of failed attempts, in 1919 the effort succeeded and (in spite of observational difficulties and marginal results) the outcome supported Einstein's theory and confirmed the idea that space curved around masses.
Spacetime curvature: Einstein ring
Since that early experiment and because of further theoretical and observational work, another prediction has been confirmed — under special circumstances in which a light source, a large mass and the earth are in precise alignment, spacetime curvature can produce something called an Einstein ring.
Figure 6: Gravitational lens geometryEinstein rings and similar optical phenomena arise from what is called gravitational lensing, consisting of light following lines of spacetime curvature, but Figure 6 shows that the resulting ray traces have little in common with an optical lens (Figure 5) — indeed, the geometry of a gravitational lens is in some ways the opposite of an optical lens.
It's important to understand about Figure 6 that it doesn't show photon paths curving through a flat background spacetime — it shows spacetime being curved by mass. The photon paths are in essence straight lines through curved spacetime.
The reason for the word "ring" in Einstein ring is that, unlike the optical lens shown in Figure 5, there is only one pathway that allows light to travel from the source to the viewer, shown in Figure 6 as blue dotted lines. Remember that Figure 6 is a flat representation of a three-dimensional system, and the blue lines represent a cylinder in three dimensions — a cylinder that the viewer sees as a ring of light.
Because of how gravitational lensing works, the requirements for a visible, complete Einstein ring are rather severe — three bodies must be in precise alignment, and the mass and location of the deflecting body must also meet strict requirements. In most cases, an astronomer will see one or more short arcs representing a light source behind a massive body, or sometimes an elongated arc resembling a horseshoe.
Spacetime curvature: simulator
Black hole mass:Figure 7: Interactive gravitational lensing diagramFor readers who want to explore the effects predicted by general relativity, Figure 7 is a gravitational curvature simulator that models a supermassive black hole deflecting the light from a background galaxy. To use the model, change the location of the black hole (red dot) by dragging your mouse across the figure, and change the black hole's mass with your mouse wheel.
The physical model in Figure 7 is correct, but it represents an unlikely set of circumstances. To get this effect in reality, a very large black hole, such as is thought to live at the center of most galaxies, would have to be moving freely between galaxies, and would have to align itself between the viewed galaxy and Earth — not very likely.
Most real Einstein rings and arcs result from one galaxy being aligned by chance with another, farther away, so that we see some of the distant galaxy's light deflected around the foreground galaxy. But so far, we haven't observed any perfect Einstein rings.
To produce an Einstein ring with Figure 7, drag the black hole (the red dot) to the position of a bright spot, two of which appear near the top center of the galaxy image. With some care, you can align the black hole over a bright spot and produce a perfect ring.
Figure 8: Black hole
spacetime curvatureEvent Horizon
Close examination of the geometry modeled by Figure 7 shows that, as one approaches a sufficiently dense, massive object, spacetime curvature increases without bound. The area nearest the black hole in Figure 7 (red dot) is empty because the spacetime curvature is greater than 90° (shown as red lines in Figure 8), so those paths don't intersect any visible objects. Even closer to the black hole, near the event horizon's radius, spacetime curvature is such that a photon will perpetually orbit the black hole.
Remember about relativity that all perceptions are local. This means that, to an observer distant from the curvature shown in Figure 8, it might be possible to observe it more or less as shown, but to an observer approaching a black hole's event horizon, instead of seeing spacetime curvature increase, the observer would instead see the event horizon's curvature decrease (assuming the horizon were visible at all). At a radius of $\frac{3}{2}r$ (r = event horizon radius), the black hole's surface would become a flat plane, infinite in extent, with eyelines extending around the horizon — indeed, in all directions at a distance of $3 \pi r$, the observer would see the back of his own head.
Microlensing
Gravitational lensing plays a part in the search for planets around other stars as well as free-roaming masses. There are a number of ways to detect a planet orbiting a star that's too distant to image directly:
- Detect a small reduction in starlight caused by a planet passing in front of the star (a method used by the Kepler spacecraft).
- Detect a shift in the spectrum of a star caused by its motion toward, and away from, the earth, as it orbits the common center of mass of itself and an orbiting planet.
- Detect a small brightening of starlight caused by a planet or other mass moving between a star and earth.
The third method in the above list is called gravitational microlensing. It's only rarely used to detect planets near a star — it's more suitable for detecting dark masses distant from stars or even galaxies. As it turns out, when a massive object passes in front of a distant star, even when the range is too great to resolve an Einstein ring, because of microlensing the amount of light received can be momentarily greater than without the intervening object. This method can be used to detect objects that emit no light of their own.
At this point it should be clear that relativity's key ideas are completely accessible and easy to understand, and it's a shame they're not better understood by nonspecialists. I say this in particular because of how often one hears the claim that superluminal space travel is just around the corner — all we need to do is find a wormhole, or a "tear in the fabric of spacetime," as any number of movie script writers have put it.
These fantasies underestimate the importance of causality in physical theory. If superluminal speeds were possible, time would lose its conventional meaning, effects could precede their causes and energy would not be conserved — apart from the fact that it opens the door to any number of temporal paradoxes.
Rather than read about how the task of jumping directly and instantaneously across the universe is only a matter of building the right spacecraft from parts available at your local hardware store, I would prefer it if people understand how this is supremely unlikely, and better, that people understand why.It's my hope that this article will serve as a brief guide to relativity's unfamiliar territory, and perhaps reduce the number of science fiction ideas that masquerade as science.
- On the electrodynamics of moving bodies, A. Einstein, 1905 — Einstein's first relativity paper.
- Special Relativity — an encyclopedia summary of the restricted version of relativity theory.
- Hermann Minkowski — Einstein's math teacher.
- Spacetime — the unification of three space dimensions, and one time dimension, into a four-dimensional entity with common properties.
- Pythagorean Theorem — a defining principle of geometry
- Photon — the carrier particle of the electromagnetic field.
- Newton's second law of motion — the net force on an object is proportional to the rate of change of its linear momentum.
- Spacetime interval — a four-dimensional spacetime distance used in causality computations.
- light cone — a visualization aid for picturing spacetime intervals.
- Causality — the relationship between causes and effects.
- Quantum entanglement — a bizarre effect of quantum theory in which two or more particles become interdependent, regardless of their spatial separation.
- General relativity — special relativity's successor theory that includes accelerations and gravitation.
- Tests of General Relativity: Deflection of light by the Sun — an early confirmation of general relativity.
- Black hole — an object so massive and dense that surface escape velocity exceeds the speed of light.
- Einstein ring — a somewhat dramatic optical manifestation of spacetime curvature.
- Gravitational lens — an effect of general relativity in which spacetime curvature produces distinct images.
- Kepler (spacecraft) — an ambitious and successful program to detect planets orbiting distant stars.
- Gravitational microlensing — an observational method that relies on spacetime curvature, moving masses, and starlight.
- Event horizon — the radius of a black hole at which escape velocity is equal to the speed of light.
- Temporal paradox — a class of logical problems associated with time travel.
| Home | | Science | |  |  |  Share This Page Share This Page |