 Share This Page
Share This Page| Home | | Science | | * Gravitation Equations | |  |  Share This Page Share This Page |
A collection of gravitational resources
— P. Lutus — Message Page —
Copyright © 2010, P. Lutus
(double-click any word to see its definition)
This article set is a gravitation resource — a handy compilation of gravitational physics descriptions, methods and equations, with some related topics like inertia and centripetal force. It addresses Newtonian gravitation, the classic first-order approximation of relativistic gravitation that is most useful in everyday gravity calculations. Some relativity facts are included when they are needed to complete a thought, for example with respect to energy, but relativity is not the primary topic.
Many of the gravitational explanations that appear here are derived from my other articles. This article unites them by topic and provides a narrative overview.
Before moving on to specific topics, let's set the stage with some key constants and ideas. Newtonian gravity is pretty easy to understand — it revolves around a handful of values and a single equation from which many others derive:
G is the universal gravitational constant. This constant is estimated to be equal to $6.67428 × 10^{-11} \frac{m^3}{kg\ s^2}$. It is also known as "Big G" to distinguish it from little-g, to be described below.
Among natural physical constants, G is not known to very high precision, in spite of its importance. This arises from the extraordinary difficulty involved in measuring it.
All other gravity equations derive from the gravitational force equation:
(1) $\displaystyle f = G \frac{m_1 m_2}{r^2}$Where:
- f = Force between masses $m_1$ and $m_2$, with units of newtons.
- G = Universal gravitational constant, described above.
- $m_1,m_2$ = Two masses in mutual attraction, units kilograms.
- r = distance between $m_1$ and $m_2$, meters.
Note that gravitational forces are almost always computed with respect to the centers of objects. For example, Earth's gravitation can be computed as though all its mass was located at a point in its center. For reasons beyond the scope of this article, for a uniform mass, this is a perfectly valid simplifying assumption.
"Little-g" is a derived value for gravitational acceleration on Earth's surface. Here is how little-g is computed:
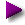
First term: Gravitational acceleration ($a_g$ in Figure 1)
Figure 1: Factors in little-gWe begin with a form of equation (1) and the following constants:
- $e_m$ = Earth's mass: 5.9736 × 1024 kilograms.
- $e_r$ = Earth's radius: 6.371 × 106 meters.
- $G$ = Described above.
This produces:
(2) $\displaystyle a_g = G \frac{e_m}{e_r^2} = 9.82257 \frac{m}{s^2} $ for small masses.The reason there is no second mass term in equation (2) is because a moving mass, when accelerated by gravity, experiences a cancellation of its own mass according to the equivalence principle, which states that gravitational force and inertial force are equal. This means Earth's mass is the only factor in the motion of a small mass, and it explains why large and small masses fall at the same rate in a gravitational field. This means whenever an acceleration is computed and with rare exception, the smaller mass is dropped from the original equation (1).
Second term: Centripetal Force ($a_c$ in Figure 1)
Result: $g = a_g - a_c$The first term above computes the gravitational acceleration at Earth' surface, but there is another factor to be taken into account — Earth's rotation produces a centripetal force. This factor makes masses near the equator experience slightly less net acceleration (and stationary masses experience slightly less force) than if they were located at the poles.
Figure 1 shows the force vectors involved in this computation. It summarizes the effects of equation (2) above, and it includes an equation for centripetal force derived from this standard one:(3) $\displaystyle f = \frac{m v^{2}}{r}$For this problem we need to write equation (3) in a way that computes an acceleration (so, as before, we drop m, the mass of the moving object). Then we need to accommodate the fact that both the effective radius and rotational velocity change at different latitudes, and finally we need to accommodate the fact that the gravitational force and the centripetal force vectors are not aligned anywhere but the equator, as shown in Figure 1.
With these facts in mind, we write this equation:
(4) $\displaystyle g = \frac{Gm}{r^2} - \frac{(v\ cos(\phi))^2}{r\ cos(\phi)} cos(\phi) = \frac{Gm}{r^2} - \frac{v^2 cos(\phi)^2}{r}$Where, in addition to terms already introduced:
- φ = latitude.
- v = Earth's equatorial velocity, about 463.3 m/s2
The resulting g value for the previously defined constants and 45° north or south latitude is approximately $9.8057 \frac{m}{s^2}$. But, because little-g has been somewhat arbitrarily defined in the literature, and to avoid producing results that differ from those in textbooks, unless otherwise noted we will be using the agreed value:
$g = 9.80665 \frac{m}{s^2}$Other factors
The above is by no means an exhaustive discussion of the issues involved in computing little-g. There is altitude, which causes gravitation to decline as the inverse square of distance, and the fact that Earth is not spherical, among others. But the above result is suitable for computing surface forces and accelerations.
Rather than use graphic images of the equations, this article uses a LaTeX rendering scheme called MathJax. It is my first article using this method. It has the advantage that I can simply type in equations and see them rendered a few seconds later (or I can visit my LaTeX editor for more complex equations). Another advantage is that when the page is scaled up, the equations look better, not worse as with graphic renderings.
This is a list of references for the entire article set.
| Home | | Science | | * Gravitation Equations | |  |  Share This Page Share This Page |